Problem 2 - Answers¶
The Monty Hall Problem
Problem statement (from the problem sheets) - canonical variation (a)¶
In a game, you can pick one of three doors, labelled A, B and C. Behind one of the three doors lies a highly desirable prize, such as the solutions to next summer’s exams. After you have chosen, but not opened, one door (e.g., door A) the person who is presenting the game opens one of the remaining two doors so as to reveal that there is no prize behind it (e.g., door C might be opened). Notice that the gameshow presenter knows that the door he opens has no prize behind it. At this point you can either stick with your original choice (door A) or switch to the door which remains closed (door B). At the end, all doors are opened, at which point you will only win if the prize is behind your chosen door. Should you stick with your choice or is it better to switch? Justify your answers.
Setup¶
%matplotlib inline
import string
from collections import Counter
from numbers import Number
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
# Homogenise matplotlib plotting.
mpl.rc("axes", grid=True)
mpl.rc("grid", linestyle="--", alpha=0.4)
mpl.rc("legend", loc="best")
Define a function which ‘plays’ the game once with an option to switch or stay¶
def monty_hall(switch=False, rng=None):
"""Return the result of one iteration of the Monty Hall problem.
Parameters
----------
switch : bool
If true, switch when the host opens on of the two remaining doors.
rng : numpy random Generator or None
Generator which can be used to make runs repeatable if given.
Returns
-------
outcome : bool
True if the winning door was guessed correctly, false otherwise.
"""
if rng is None:
# Initialise the random number generator.
rng = np.random.default_rng()
# We want 3 doors.
doors = tuple(string.ascii_uppercase[:3])
# To make debugging easier, we can use the door names 'A', 'B', and 'C' directly.
# Choose the door containing the prize.
prize_door = rng.choice(doors)
# Choose a door randomly.
chosen_door = rng.choice(doors)
# The host opens one of the remaining doors randomly, provided there is no prize behind it.
remaining_doors = [door for door in doors if door not in (chosen_door, prize_door)]
open_door = rng.choice(remaining_doors)
# Depending on the `switch` option, switch.
if switch:
# Calculate the doors which are available, i.e. not opened.
available_doors = [
door for door in doors if door not in (open_door, chosen_door)
]
assert len(available_doors) == 1
chosen_door = available_doors[0]
# Determine the outcome.
return chosen_door == prize_door
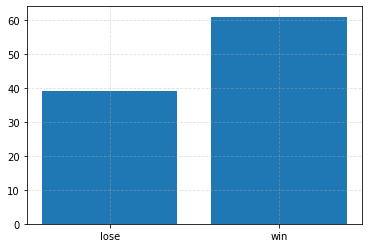
Play the game without switching¶
# Make runs repeatable.
rng = np.random.default_rng(0)
# Play the game multiple times.
outcomes = [monty_hall(rng=rng) for i in range(100)]
plt.figure(figsize=(6, 4))
plt.bar(*zip(*Counter(outcomes).items()))
_ = plt.xticks([0, 1], ["lose", "win"])
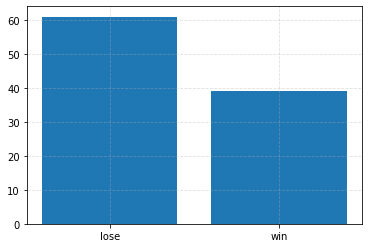
Play the game with switching¶
# Make runs repeatable.
rng = np.random.default_rng(0)
# Play the game multiple times.
outcomes = [monty_hall(switch=True, rng=rng) for i in range(100)]
plt.figure(figsize=(6, 4))
plt.bar(*zip(*Counter(outcomes).items()))
_ = plt.xticks([0, 1], ["lose", "win"])
Problem statement (from the problem sheets) - variation (b)¶
In a variation, after you have chosen door A, you are given the choice to open one of the remaining doors B or C. Notice that this time, the person opening the door does not know whether the prize is behind it or not. You pick door C, and upon opening it you discover there is nothing behind it. At this point you are again free to either stick with door A or to switch to door B. Are the probabilities different from the previous scenario? Justify your answers.
def monty_hall_b(switch=False, rng=None):
"""Return the result of one iteration of the varied Monty Hall problem.
Parameters
----------
switch : bool
If true, switch again after having opened one door without winning.
rng : numpy random Generator or None
Generator which can be used to make runs repeatable if given.
Returns
-------
outcome : bool
True if the winning door was guessed correctly, false otherwise.
"""
if rng is None:
# Initialise the random number generator.
rng = np.random.default_rng()
# We want 3 doors.
doors = tuple(string.ascii_uppercase[:3])
# To make debugging easier, we can use the door names 'A', 'B', and 'C' directly.
# Choose the door containing the prize.
prize_door = rng.choice(doors)
# Choose a door randomly.
chosen_door = rng.choice(doors)
# Pick a second door such that no prize is behind it.
second_chosen_door = rng.choice(
[door for door in doors if door not in (prize_door, chosen_door)]
)
if second_chosen_door == prize_door:
# If the correct door was picked, the game is won!
return True
# Since the prize was not behind `second_chosen_door`, one now has the option
# between sticking with the original `chosen_door`, or switching.
if switch:
# Calculate the doors which are available, i.e. not opened.
available_doors = [
door for door in doors if door not in (chosen_door, second_chosen_door)
]
assert len(available_doors) == 1
chosen_door = available_doors[0]
# Determine the outcome.
return chosen_door == prize_door
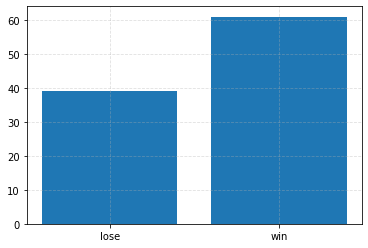
Play the game without switching¶
# Make runs repeatable.
rng = np.random.default_rng(0)
# Play the game multiple times.
outcomes = [monty_hall_b(rng=rng) for i in range(100)]
plt.figure(figsize=(6, 4))
plt.bar(*zip(*Counter(outcomes).items()))
_ = plt.xticks([0, 1], ["lose", "win"])
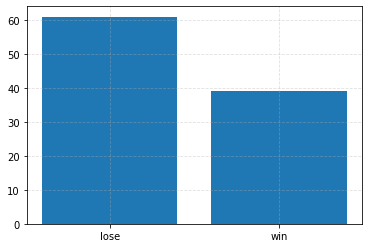
Play the game with switching¶
# Make runs repeatable.
rng = np.random.default_rng(0)
# Play the game multiple times.
outcomes = [monty_hall_b(switch=True, rng=rng) for i in range(100)]
plt.figure(figsize=(6, 4))
plt.bar(*zip(*Counter(outcomes).items()))
_ = plt.xticks([0, 1], ["lose", "win"])