Problem 4¶
An asteroid has been spotted heading towards Earth. It is your task to determine how much of a risk it poses, using the simulation techniques we developed in the previous part.
The asteroid is currently estimated to be at a distance \(r=1000R_\mathrm{E}\) from the Earth, where \(R_\mathrm{E}=6371\)km is the radius of the Earth. It’s at due NW, an angle of \(\theta=3\pi/2\) from the \(x\)-axis. It’s travelling with a radial speed of \(v_\mathrm{r}=-1000\)m/s and a tangential speed of \(v_\mathrm{t}=15\)m/s, where the radial vector points away from the Earth and the tangent vector points anti-clockwise. The below diagram illustrates the coordinate system.
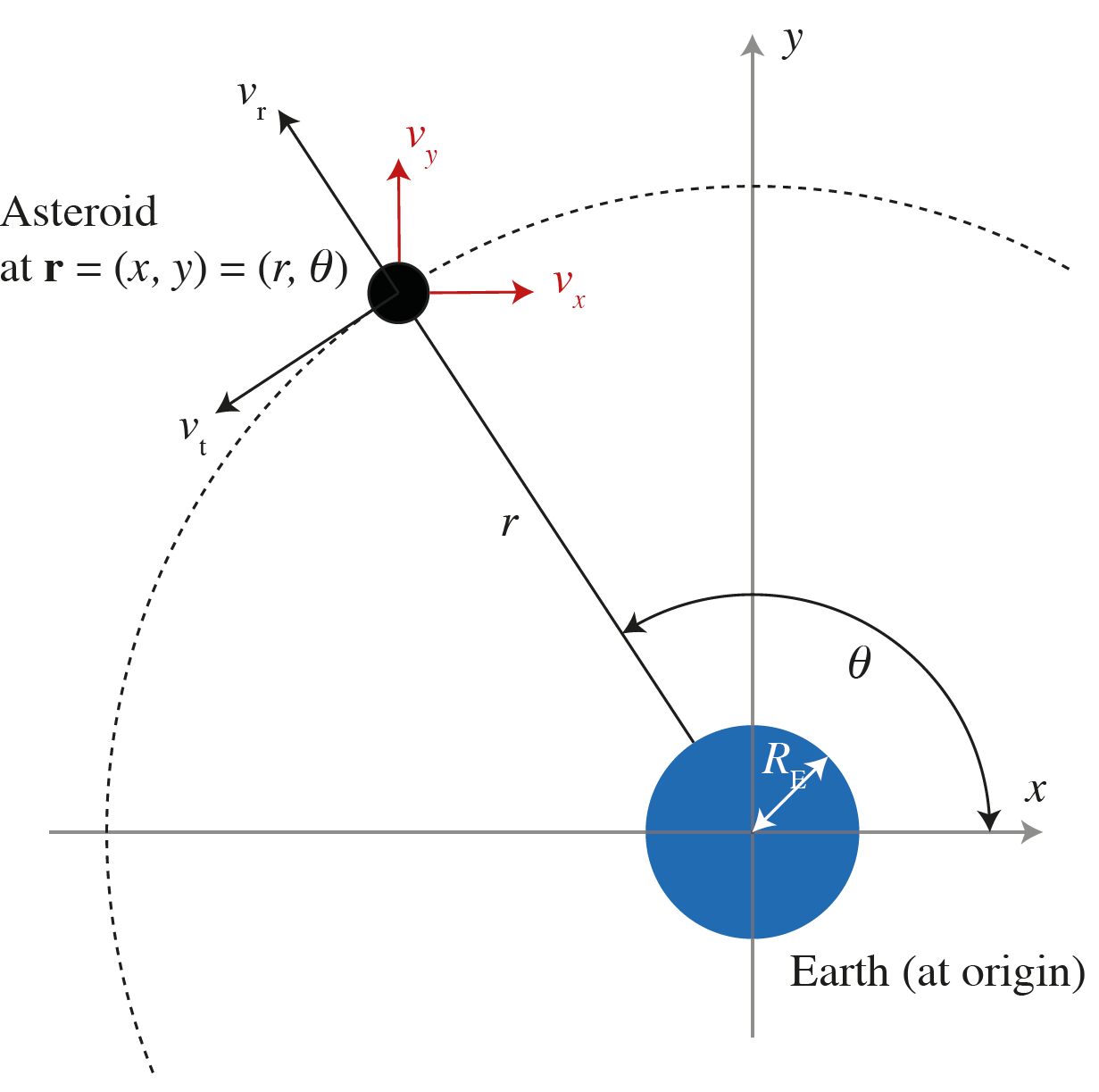
Fig. 2 The coordinate system for this problem.¶
Using the same simulation technique from the previous part, answer the following questions. Make sure first that you can easily convert between the Cartesian coordinates needed in the simulation and the polar coordinates we have used to define the initial conditions.
Closest Approach¶
Using the initial conditions above, run a simulation and determine the closest point of approach for the asteroid. How long have we got until this occurs? What speed does the asteroid have at this point? The below figure shows what the orbit should look like.
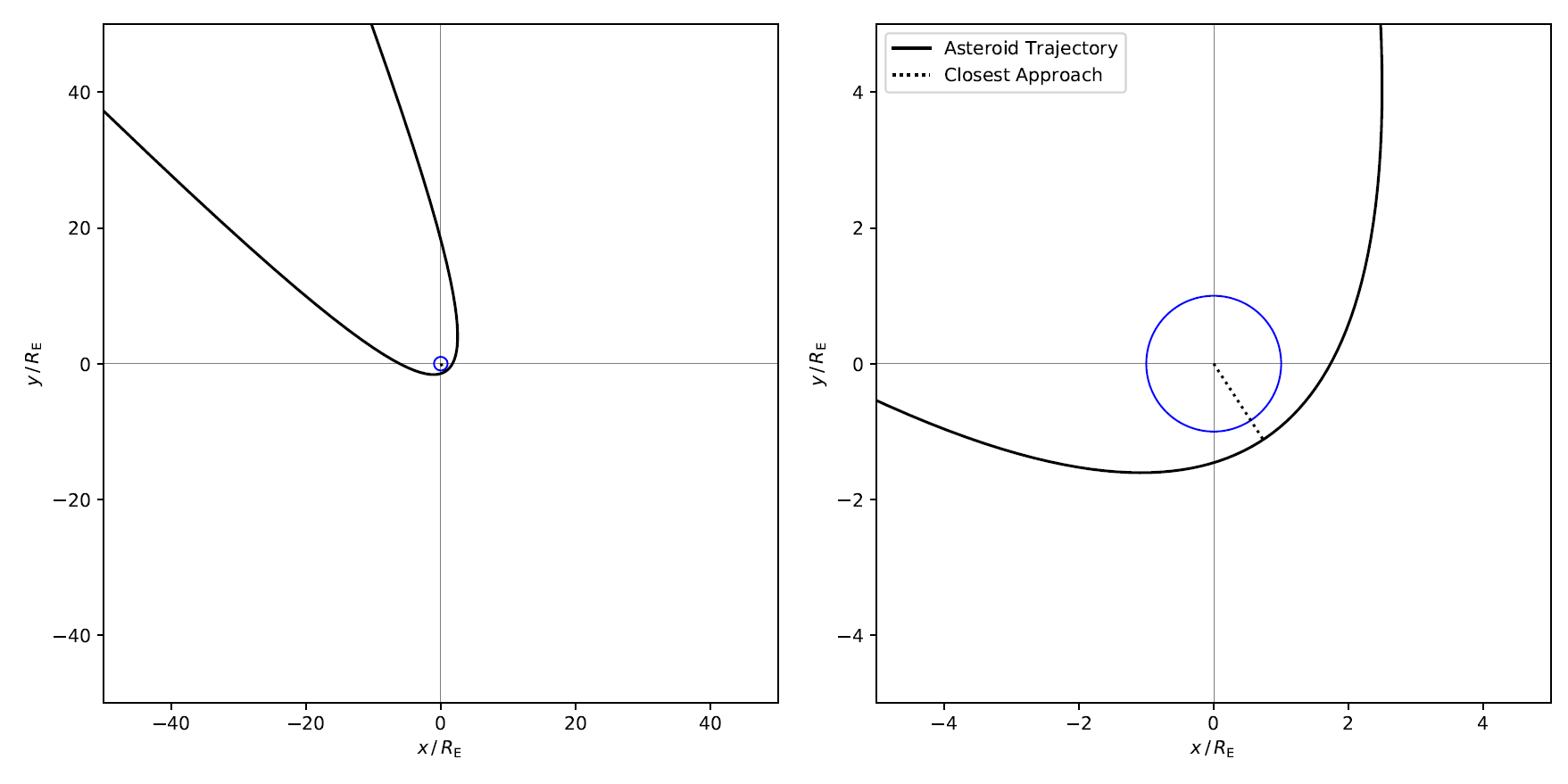
Fig. 3 The trajectory for the initial conditions. Earth is drawn to scale. Note the difference in axis limits.¶
Impact Probability¶
The initial conditions we have for the asteroid predict that it will pass closely by the Earth, but not impact. However, those initial conditions are from telescope measurements which have uncertainties. The radial distance has a \(15\%\) uncertainty, i.e., it is measured as \(r=(1000\pm150)R_\mathrm{E}\). Using this, calculate the percentage chance that the asteroid will impact the Earth. Plot all of the sample orbits on the same figure to see how the change in initial position effects the orbit. The below figure shows an example.
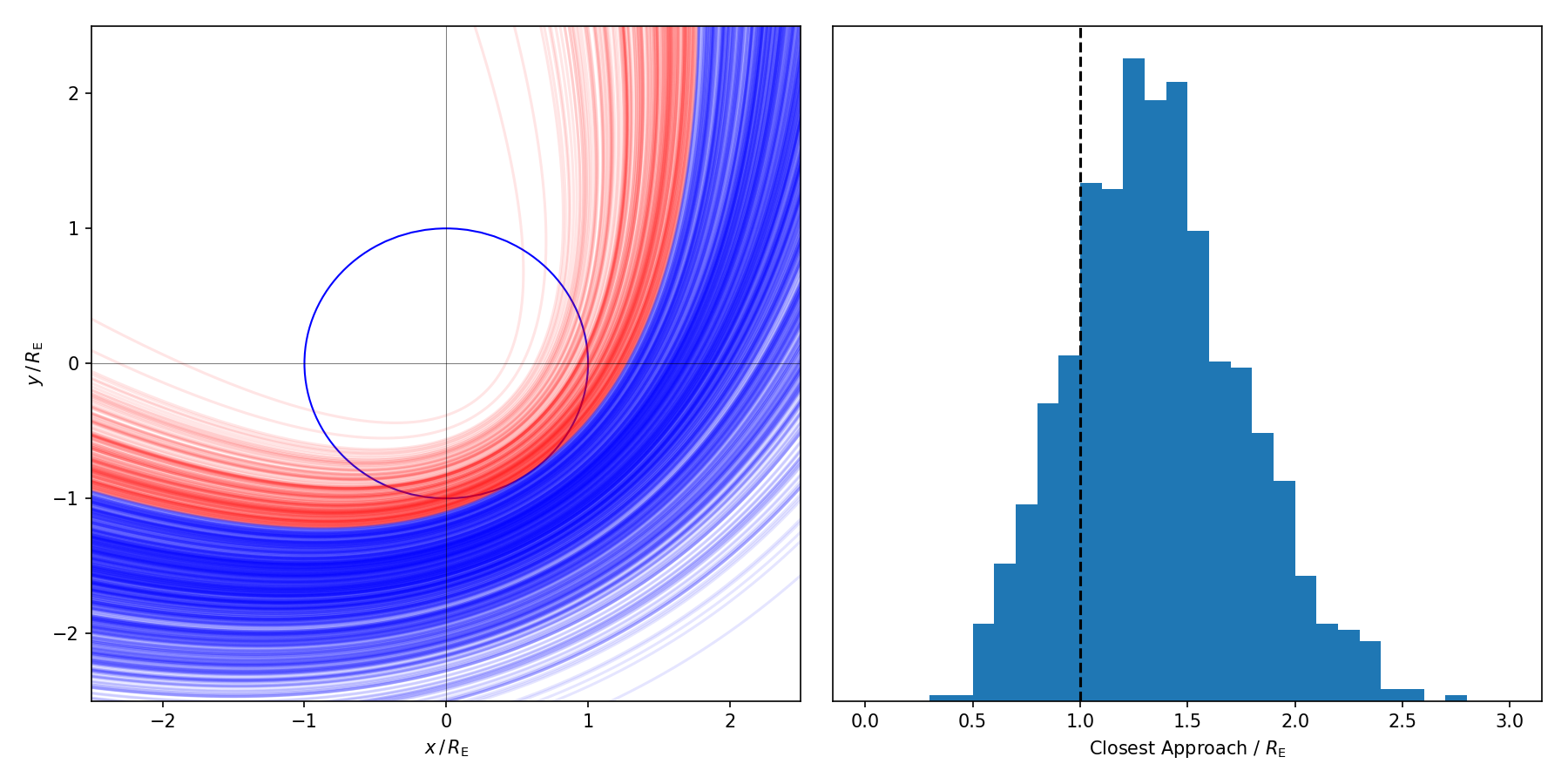
Fig. 4 The distribution of trajectories for a \(15\%\) error in initial radius. All trajectories to the left of the black dashed line will collide.¶
Hint
Use numpy.random.normal to get a normal distribution centred on \(r=1000R_\mathrm{E}\) with standard deviation \(\sigma_r=150R_\mathrm{E}\). In a for loop, run a simulation for every initial radial position in the distribution. Determine the condition for a trajectory to collide with the Earth and find how many of these occur.
Avoiding Impact¶
We have now obtained new data that confirms the asteroid is at exactly \(r=750R_\mathrm{E}\). This puts it on a direct collision trajectory. A plan has been proposed to divert the asteroid’s course. A rocket will intercept the asteroid when the asteroid is at \(r=60R_\mathrm{E}\), releasing at \(r=40R_\mathrm{E}\). While attached, the rocket will boost the asteroid’s velocity in the direction perpendicular to its current velocity, and away from the Earth, i.e., if the asteroid is travelling in the SE direction, the rocket boosts it SW. Determine the necessary boost to the asteroid’s velocity to successfully prevent it from colliding with Earth. The below figure shows an example of the trajectories you should see from the given range of boosts.
Hint
You will need to modify the update_function so that, when in the correct radial range, the asteroid’s velocity is boosted by a certain amount. Choose a range of velocity amounts and perform a simulation for each to find which collide.

Fig. 5 The trajectories resulting from the boost indicated on the colourbar.¶
